티스토리 뷰
어떻게 생각하면 지난 N-Queens 알고리즘이 좀 더 어렵다고 생각할 수도 있겠지만, 이번 멱집합도 만만치는 않은 것 같다. 일단 수학 공부를 손에서 뗀 지 꽤 지난 시점이다 보니 수학적인 이해를 동반해야 하고, 거기에 가장 난감한 재귀함수적인 사고로 재귀함수적인 알고리즘을 짜내야 하기 때문에 복합적으로 작용이 되어 난도가 많이 올라간 것 같다는 느낌이 든다. 그렇지만 최대한 정리해보고자 한다.
멱집합?
Powerset
집합 A={a, b, c, d}가 있다.
집합 A가 구성할 수 있는 부분집합의 수는 2^4=16개이다.
{Ø} => 1개
{a}, {b}, {c}, {d} => 4개
{a, b}, {a, c}, {a, d}, {b, c}, {b, d}, {c, d} => 6개
{a, b, c}, {a, b, d}, {a, c, d}, {b, c, d} => 4개
{a, b, c, d} => 1개
- 그런데 여기서 {a, b, c, d}에서 모든 부분집합을 나열하기 위해서는
- a를 제외한 {b, c, d}의 모든 부분집합을 나열하고 (2^3=8개)
- { } => 1개
- {b}, {c}, {d} => 3개
- {b, c}, {b, d}, {c, d} => 3개
- {b, c, d} => 1개
- {b, c, d}의 모든 부분집합에 {a}를 추가한 집합을 나열한다. (2^3=8개)
- {a} => 1개
- {a, b}, {a, c}, {a, d} => 3개
- {a, b, c}, {a, b, d}, {a, c, d} => 3개
- {a, b, c, d} => 1개
- 1번과 2번에서 나온 개수를 합하면 16개가 된다. 따라서 {a, b, c, d}의 부분집합의 개수는 16개이다.
- a를 제외한 {b, c, d}의 모든 부분집합을 나열하고 (2^3=8개)
위와 같이도 식이 도출될 수 있다.
이러한 성질을 이용하고 또 재귀적인 부분을 찾아 재귀함수를 직접 구현해보도록 하겠다.
문제 확인
집합 A={a,b,c,d}가 있다. 부분집합을 모두 출력하시오.
- {a, b, c, d}에서 모든 부분집합을 나열하기 위해서
- a를 제외한 {b, c, d}의 모든 부분집합을 나열하고 (2^3=8개)
- b를 제외한 {c, d}의 모든 부분집합을 나열하고 (2^2=4개)
- c를 제외한 {d}의 모든 부분집합을 나열하고 (2^1=2개)
- d를 제외한 {}의 모든 부분집합을 나열하고 (2^0=1개)
- {}의 부분 집합에 {d}를 추가한 집합을 나열한다. (2^0=1개)
- {d}의 모든 부분 집합에 {c}를 추가한 집합을 나열한다. (2^1=2개)
- c를 제외한 {d}의 모든 부분집합을 나열하고 (2^1=2개)
- {c, d}의 모든 부분 집합에 {b}를 추가한 집합을 나열한다 (2^2=4개)
- b를 제외한 {c, d}의 모든 부분집합을 나열하고 (2^2=4개)
- {b, c, d}의 모든 부분 집합에 {a}를 추가한 집합을 나열한다. (2^3=8개)
- a를 제외한 {b, c, d}의 모든 부분집합을 나열하고 (2^3=8개)
재귀의 성질을 이용하면 위와 같이 구현을 할 수 있는 것이다.
public class PowerSet {
private static char data[]= {'a','b','c','d'};
private static int n=data.length;
private static boolean[] include = new boolean[n];
public static void powerSet(int k) {
System.out.format("powerSet(%d) 호출됨.\n",k);
if(n==k) {
for(int i=0;i<n;i++) {
if(include[i]) System.out.print(data[i]+" ");
}
System.out.println();
return;
}
System.out.format("집합 %c 원소는 미포함한 부분집합 구하기 powerSet(%d)\n", data[k], k+1);
include[k]=false;
powerSet(k+1);
System.out.format("집합 %c 원소를 포함시킨 부분집합 구하기 powerSet(%d)\n", data[k],k+1);
include[k]=true;
powerSet(k+1);
}
public static void printArray() {
for(char c: data) {
System.out.format("%c ",c);
}
System.out.println();
}
public static void main(String[] args) {
powerSet(0);
}
}
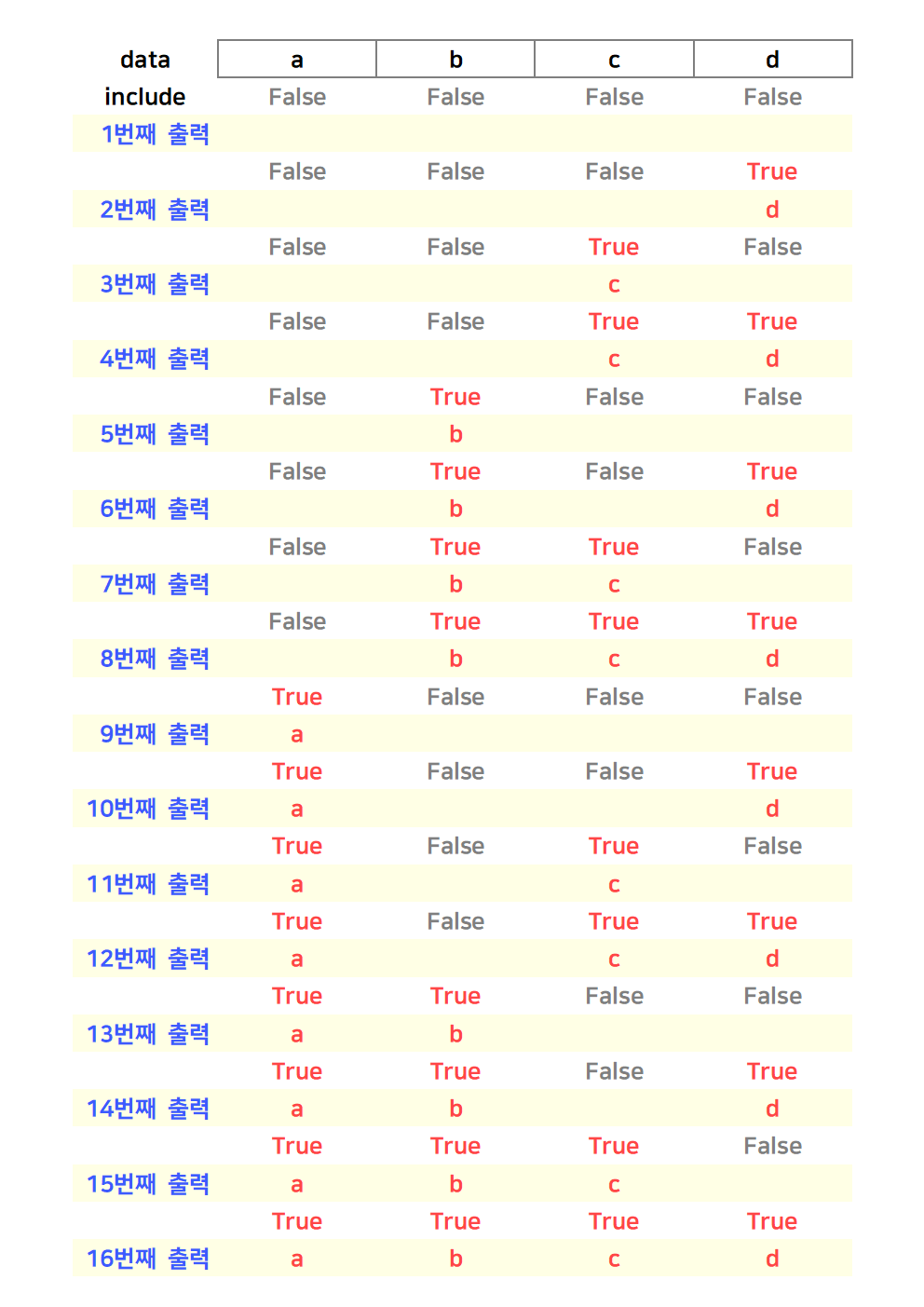
결과 화면
powerSet(0) 호출됨.
집합 a 원소는 미포함한 부분집합 구하기 powerSet(1)
powerSet(1) 호출됨.
집합 b 원소는 미포함한 부분집합 구하기 powerSet(2)
powerSet(2) 호출됨.
집합 c 원소는 미포함한 부분집합 구하기 powerSet(3)
powerSet(3) 호출됨.
집합 d 원소는 미포함한 부분집합 구하기 powerSet(4)
powerSet(4) 호출됨.
집합 d 원소를 포함시킨 부분집합 구하기 powerSet(4)
powerSet(4) 호출됨.
d
집합 c 원소를 포함시킨 부분집합 구하기 powerSet(3)
powerSet(3) 호출됨.
집합 d 원소는 미포함한 부분집합 구하기 powerSet(4)
powerSet(4) 호출됨.
c
집합 d 원소를 포함시킨 부분집합 구하기 powerSet(4)
powerSet(4) 호출됨.
c d
집합 b 원소를 포함시킨 부분집합 구하기 powerSet(2)
powerSet(2) 호출됨.
집합 c 원소는 미포함한 부분집합 구하기 powerSet(3)
powerSet(3) 호출됨.
집합 d 원소는 미포함한 부분집합 구하기 powerSet(4)
powerSet(4) 호출됨.
b
집합 d 원소를 포함시킨 부분집합 구하기 powerSet(4)
powerSet(4) 호출됨.
b d
집합 c 원소를 포함시킨 부분집합 구하기 powerSet(3)
powerSet(3) 호출됨.
집합 d 원소는 미포함한 부분집합 구하기 powerSet(4)
powerSet(4) 호출됨.
b c
집합 d 원소를 포함시킨 부분집합 구하기 powerSet(4)
powerSet(4) 호출됨.
b c d
집합 a 원소를 포함시킨 부분집합 구하기 powerSet(1)
powerSet(1) 호출됨.
집합 b 원소는 미포함한 부분집합 구하기 powerSet(2)
powerSet(2) 호출됨.
집합 c 원소는 미포함한 부분집합 구하기 powerSet(3)
powerSet(3) 호출됨.
집합 d 원소는 미포함한 부분집합 구하기 powerSet(4)
powerSet(4) 호출됨.
a
집합 d 원소를 포함시킨 부분집합 구하기 powerSet(4)
powerSet(4) 호출됨.
a d
집합 c 원소를 포함시킨 부분집합 구하기 powerSet(3)
powerSet(3) 호출됨.
집합 d 원소는 미포함한 부분집합 구하기 powerSet(4)
powerSet(4) 호출됨.
a c
집합 d 원소를 포함시킨 부분집합 구하기 powerSet(4)
powerSet(4) 호출됨.
a c d
집합 b 원소를 포함시킨 부분집합 구하기 powerSet(2)
powerSet(2) 호출됨.
집합 c 원소는 미포함한 부분집합 구하기 powerSet(3)
powerSet(3) 호출됨.
집합 d 원소는 미포함한 부분집합 구하기 powerSet(4)
powerSet(4) 호출됨.
a b
집합 d 원소를 포함시킨 부분집합 구하기 powerSet(4)
powerSet(4) 호출됨.
a b d
집합 c 원소를 포함시킨 부분집합 구하기 powerSet(3)
powerSet(3) 호출됨.
집합 d 원소는 미포함한 부분집합 구하기 powerSet(4)
powerSet(4) 호출됨.
a b c
집합 d 원소를 포함시킨 부분집합 구하기 powerSet(4)
powerSet(4) 호출됨.
a b c d

'컴퓨터 공부방 > 알고리즘' 카테고리의 다른 글
| 알고리즘 정렬 시간복잡도 정리 (0) | 2019.09.14 |
|---|---|
| N-Queens 여왕 알고리즘 with JAVA (0) | 2019.09.12 |
| Blob 셀 개수 세기 알고리즘 (재귀함수 응용) - JAVA (0) | 2019.09.11 |
| 미로찾기 알고리즘 (재귀함수 응용문제) JAVA (1) | 2019.09.10 |
| 재귀함수 (Recursion) 개념 및 특성 (0) | 2019.09.08 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- 개발자
- 정렬
- BLOB
- 국가기간전략직종훈련
- 영문법
- 부분집합
- 보고서
- 웹개발자
- 해커스매거진
- 미로찾기
- 청년구직활동지원금
- 알고리즘
- N-Queens
- 보고서양식
- 데이터베이스
- 20대
- 재귀함수
- 퀵정렬
- java
- 반응형레이아웃
- 멱집합
- ORM
- 대학생
- 국비지원교육
- html5
- 시간복잡도
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
글 보관함
